快速傅里叶变换（FFT）通俗入门

【写在前面】 这篇文章写给尚未系统性学习信号理论的读者，主要使用通俗的语言描述FFT在信号处理中的应用。本文原面向参加大学生电子设计竞赛的大学一年级学生，使其快速理解信号处理算法，并能在单片机、FPGA等设备上使用FFT。如果你希望了解FFT算法原理和优化等内容，不妨阅读更专业的文章或书籍。

1. 信号的频域分析

1.1 什么是频域、频谱

这是一个我们通常说的正弦波：

如果给这个图像加上坐标轴，就是一个横轴为时间 ，纵轴为电压 （或者说振幅 ）的图像:

我们叫它正弦信号的 时域 表示，从图像中可以看出不同时间点的信号振幅。

在现实生活中，我们遇到的信号通常不这么简单，可能是很多不同频率和幅度的正弦波的叠加，也可能是杂乱无章的波形。这时，如果我们想要了解一个复杂信号是由哪些简单信号组成的，就可以对信号做“傅里叶变换”（FT）。

FT结果的横轴为角频率 ，纵轴 是一个与频率有关的复数。图像中不为0的地方，就表示信号中含有对应频率的信号分量，其纵坐标代表分量成分的多少。我们把正弦波视为单频信号，它的频谱只含有一个“峰”。这就是信号的 频域 表示，我们把这样的图像叫做 频谱 ，更精确地叫它幅度谱。

1.2 FFT是做什么的

通俗地来说，傅里叶变换（FT）是把信号从 时域 变换到 频域 。它以正弦波为基准，把信号分解成一系列不同频率的正弦信号 叠加 ，好让我们分析一个信号的频率组成。我们今天讨论的快速傅里叶变换（FFT）就是从朴素的FT中逐步发展而来的。

通过对频谱进行分析，我们可以得到信号的类型、频率分量，以及不同频率所占的幅度。从变换结果中还可以计算出 相位谱 ，可以提取出不同频率分量的相位。如果变换的对象是多个信号的混合，还可以从混合信号中分离不同信号。

FT在应用于工程领域的过程中，还催生出了很多优化方法和新的思路。比如，我们分解信号所使用的基准并不一定是正弦波。“小波变换”就使用一系列被称为“小波”的基准，来表示信号的特征。这些新的发展解决了传统FT的一些局限，使得我们能够从更多的角度分析不同情景下的信号。

1.3 常见信号的频谱

正弦信号是单频信号，它频谱的单峰 就是正弦波的频率。方波和三角波都是复合信号。以方波为例，它的频谱除了 基频 之外，还有 、 ……等 谐波 分量。方波只有奇次谐波，三角波有各次谐波。

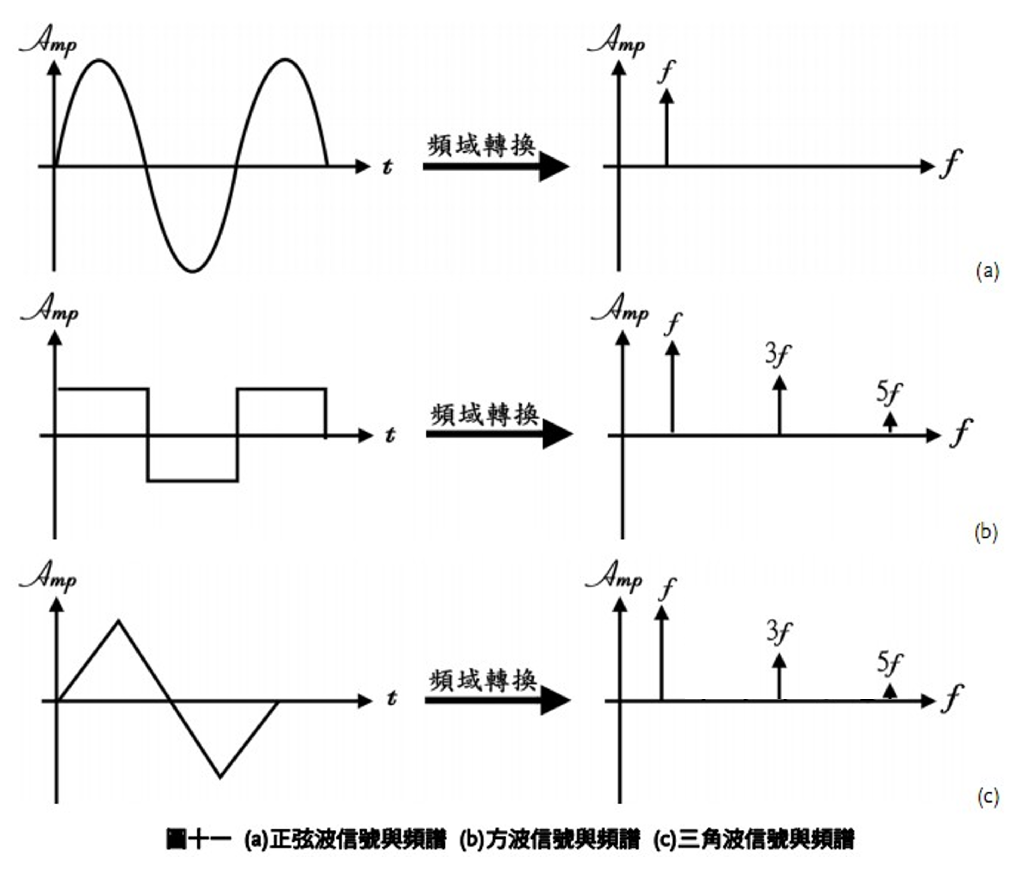
你可以理解为，方波是由一个频率 的正弦波叠加一个幅度稍小的频率 的正弦波，再叠加上更小的频率 的正弦波……这样叠加而成的。这种叠加的数学依据可以参考傅里叶级数。

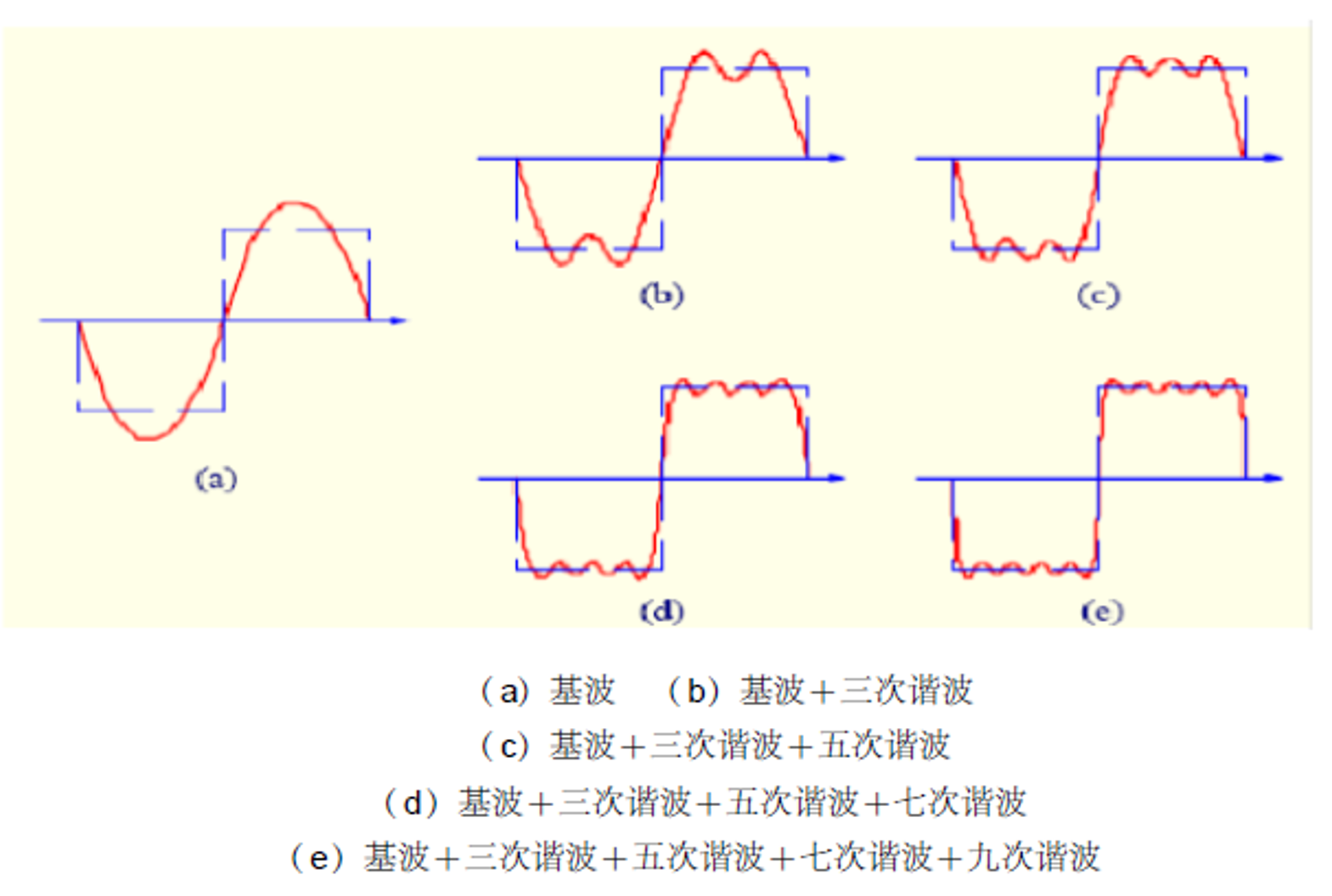
2. FFT算法

这一部分介绍FFT算法在信号处理中的使用。考虑到本文面向的读者，下文中很多定理、结论均为不加证明地给出。对于这些理论，互联网上有非常多优秀的讲解，感兴趣时不妨阅读几篇。

2.1 采样与采样定理

生活中的信号大多是模拟信号，是电压连续变化形成的。但计算机系统只能处理离散的数值，如果我们每隔一小段时间记录一次电压值，就能把连续的模拟信号变成一系列分散的数值点，这就是 采样。

采样的频率简称采样率 ，指单位时间内，信号被采样的次数。如果信号频率1kHz，采样率10kHz，那么一个周期内信号能被采样10次，即10个点。

对于信号频率与采样率的关系，奈奎斯特-香农采样定理 给出了以下要求：

“采样频率要大于信号最高频率的 2倍，才能无失真的保留信号的完整信息”

如果刚好符合采样定理的要求，那么一个周期里只有2个点，而且通常不在峰值处，连起线来仿佛成了三角波。这样的采样结果也足以提取出信号的信息，但必须从变换后的频域来分析。

2.2 FFT的结果

如果我们对一个信号做 “ 点的FFT”，会得到一个长度为 的数据序列，对应着 频率上的信号分量。

在现实生活中，我们接触的信号都是实信号（虚部为0的信号）。对于一个实信号，FFT得到的结果都是复数，需要对其取模，才能得出幅度谱。取模后的结果需要进行幅度修正，非直流分量需乘以 ，直流分量（ 处）乘以 。

需要注意的是，计算出的幅度谱仍不能准确反映信号的频率成分，会有频谱泄露、栅栏效应等偏差。我们将会在 2.3 和 2.4 节讨论这些偏差以及它们的解决方法。

下图是一个100Hz的正弦信号幅度谱，FFT点数 为512，采样率 为1kHz。

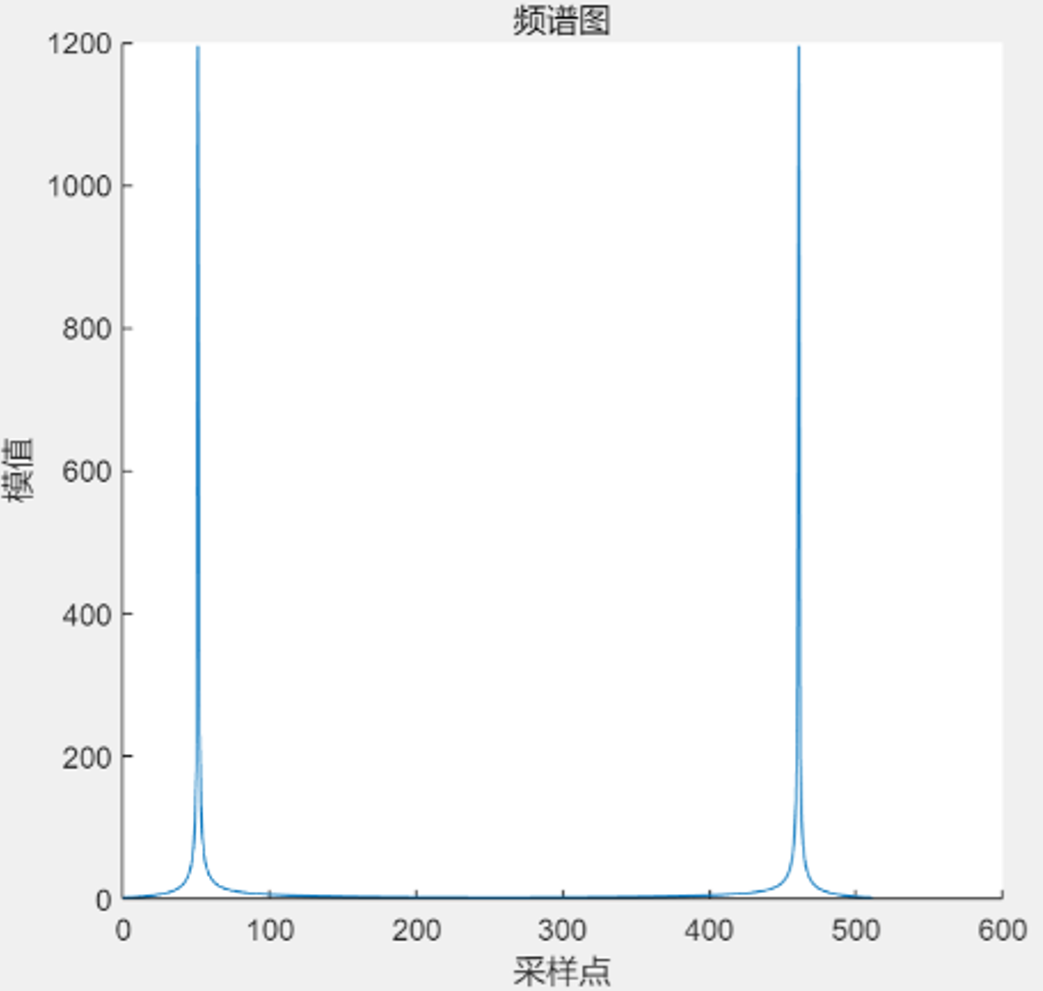
可见它是一个横轴长度为 个点，以 为轴对称的图像，从左到右对应 频率。然而，图中只有 的一段有实际意义，另一半是完全对称的图像。这也对应了奈奎斯特采样定理的要求，当信号频率大于 时，频谱就会发生混叠。高频信号会同时出现在图像的左右两侧，无法分辨其真实所处的位置。

FFT分辨率 描述了频谱横轴上的 个点与频率 的对应关系，可以理解为横轴每两个点间隔的频率。要用横坐标还原出频率，只需要乘上分辨率 。

我们可以用公式描述幅度谱和相位谱的计算方法：

对FFT结果中的每一个值，用 表示实部， 表示虚部。设 代表 中的某个点（也称频率的离散索引），则模值 可由下式计算：

类似的，求相位谱需要求复数的相位角，即

2.3 频谱泄露和窗函数

理想情况下，正弦信号的频谱应该只有两个单峰。而我们如果观察刚才这幅频谱图，会看到峰值的两侧像小山一样逐渐下降，同时整个频谱上也散布着很小的一个幅值。这种现象叫 频谱泄露，可以理解为峰值处的能量有少部分泄露到了其他频段上。

频谱泄露的原因是，FFT 由离散傅里叶变换 DFT 发展而来，但 DFT 要求信号是周期的，即最后一个采样点必须和第一个点在时域上接续。这种条件只有在采样率刚好是信号频率的整数倍时才能满足，这在现实中是难以达到的。

下面两幅图分别展示了信号周期接续和不接续的情况。

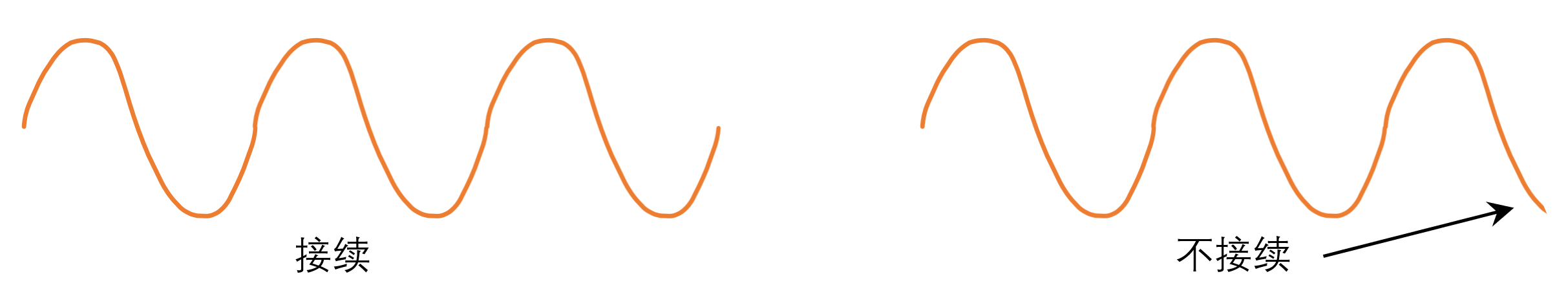
解决频谱泄露的方法是加 窗函数。我们在对信号采 个点时，其实是把连续的信号截出一部分做 FFT，这个“截”实际上就是乘以窗函数。直接采 个点，其实是乘以“矩形窗”，即采样范围内为1，其余为0的窗。习惯上我们也称这种情况为不加窗。

为了解决频谱泄露，要使最后一个采样点和第一个点在时域上接续。于是很多经典的窗函数诞生了：

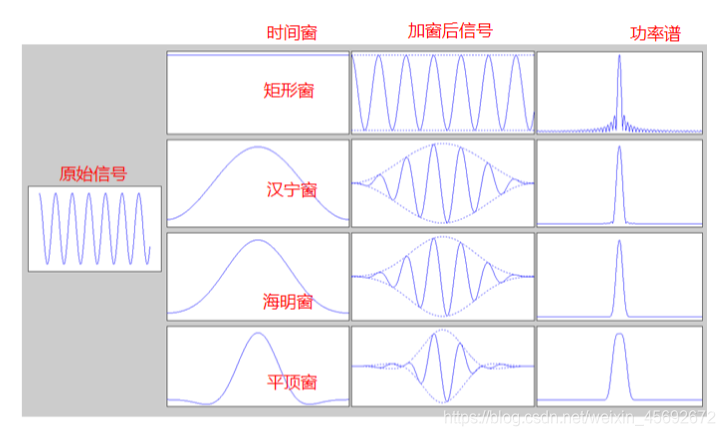
它们的特点是两边的窗系数逐渐减小，以削弱信号两端的幅度，达到前后接续的效果。其中平顶窗的特点是让频谱峰值处变成有两个或多个点的平顶状。加窗后，FFT结果的幅值会出现不同程度的衰减，需要乘上不同窗函数的恢复系数来矫正。

不同的窗适合计算不同的参数。求信号 频率 时，不加窗（矩形窗）比较准确。求 幅值 时，平顶窗比较准确。求 THD（总谐波失真）时，凯泽窗比较准确。如果需要求同一个信号的不同参数，可以加不同的窗函数多次进行FFT，以求出最准确的结果。

2.4 栅栏效应

如果对100Hz正弦信号以980Hz采样率采样，并做64点的 FFT，就会得到下面的结果：

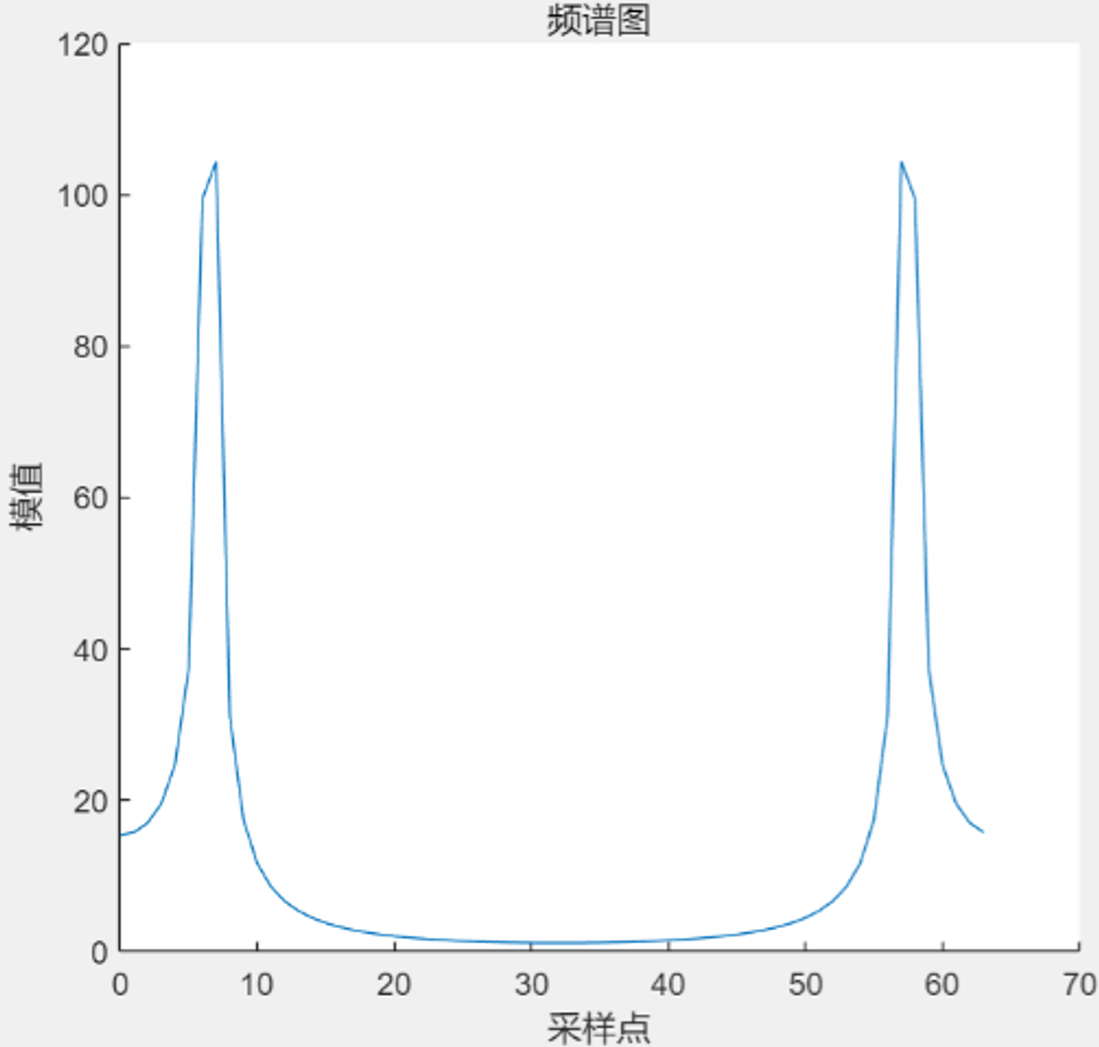
图中峰值处几乎有两个幅值相同的点。这种现象的原因是频谱分辨率 过大，也就是频谱横轴每两个点对应的频率间隔太大，信号频率恰好处于两个点之间。这就像透过一个栅栏看东西，一部分被挡板挡住，所以叫 栅栏效应。

缓解栅栏效应就要降低 。因为 ，可以降低采样率或者增加FFT点数。但因为计算资源和采样时间的限制，FFT点数不能太大，所以一般将采样率控制在信号最高频率的2.5倍左右即可。

2.5 混叠

频谱混叠 就是当采样率不满足奈奎斯特采样定理时，高频信号的频谱出现在低频区段的现象。下图可以让我们感受采样率不足时，采样结果在时域的变化。

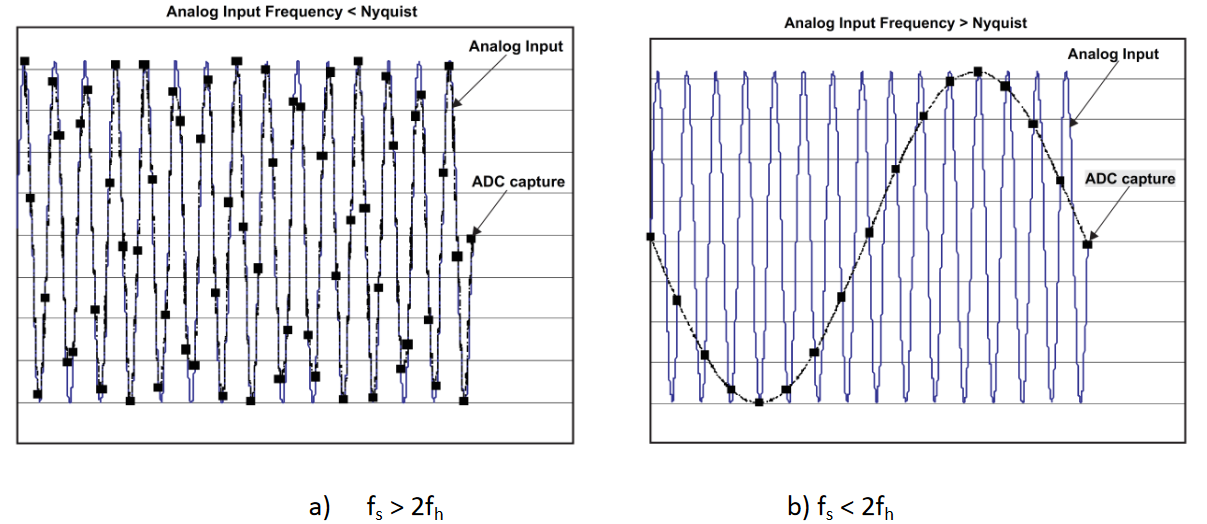
图中蓝线表示原信号，黑点和黑线表示采样结果。左侧图像代表满足采样定理时的结果,右侧则是采样率不足时的结果。可见高频信号被采样成了一个频率更低，幅值相同的信号。这就是高频信号混叠至低频的时域表现，我们称它为 欠采样。当信号欠采样且采样率为信号频率的整倍数时，采样结果有时甚至会变成DC直流信号。

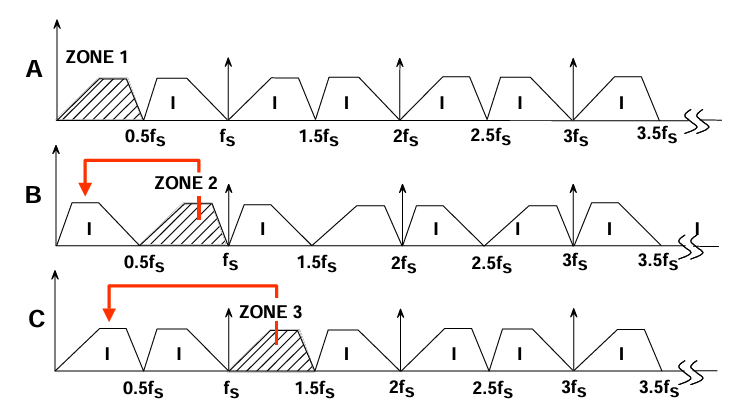
再从频域上来观察，从图中可见频谱混叠并不局限于 的区段，每个区间内的信号都会像“照镜子”一样，反映在其他区间的相应位置上。实质上，采样就是对信号的频谱以 为周期进行搬移的过程，混叠就是信号频谱在搬移过程中产生了重叠。

在通信领域，信号通常会被调制到频率更高的载波上传递，这时我们很难达到奈奎斯特采样定理所要求的采样频率。不过，这类信号虽然总体频率很高，但在频谱中所占的宽度（信号带宽）通常不大。如果我们能利用采样带来的频谱搬移，同时保证这样的搬移不会导致频谱重叠，就能转而分析原信号在低频段的镜像频谱。我们把这种方法叫做 “带通采样” ，把之前提到的方法叫做 “低通采样”。

如果你想了解关于采样和混叠更详细的介绍，还可以阅读Analog Devices公司编写的MT-002指南：《奈奎斯特准则对数据采样系统设计有何意义》。

3. FFT在STM32上的实现

ST官方的 CMSIS DSP 库中提供了多种FFT实现，常用的有处理实信号的 arm_rfft_fast_f32 和处理复信号的 arm_cfft_f32。库中也提供了 arm_cmplx_mag_f32 函数来对FFT输出的复数数据取模。另外，ST也提供使用汇编语言编写的版本 cr4_fft_X_stm32（X为FFT点数）。

我们生活中处理的信号都是实信号，使用面向实信号的函数能加快运算速度。同时，这些函数有不同的数据格式，具体的使用方法可以参考 CMSIS DSP 库官方文档和互联网上的资料。

关于FFT的介绍就到这里了，感谢你读完这篇文章！如果文中出现了任何错误，或者你想深入讨论某个知识点，欢迎在评论区留言~

4. 参考资料

实战数字信号处理之三 - 从FFT得到幅值和相位信息
FFT与窗函数：信号分析中的关键技术
带通采样定理及其公式推导
Analog Devices - 奈奎斯特准则对数据采样系统设计有何意义
CMSIS DSP Software Library